经典动态规划问题:高楼扔鸡蛋(进阶)
上篇文章聊了高楼扔鸡蛋问题,讲了一种效率不是很高,但是较为容易理解的动态规划解法。后台很多读者问如何更高效地解决这个问题,今天就谈两种思路,来优化一下这个问题,分别是二分查找优化和重新定义状态转移。
如果还不知道高楼扔鸡蛋问题的读者可以看下「经典动态规划:高楼扔鸡蛋」,那篇文章详解了题目的含义和基本的动态规划解题思路,请确保理解前文,因为今天的优化都是基于这个基本解法的。
二分搜索的优化思路也许是我们可以尽力尝试写出的,而修改状态转移的解法可能是不容易想到的,可以借此见识一下动态规划算法设计的玄妙,当做思维拓展。
二分搜索优化
之前提到过这个解法,核心是因为状态转移方程的单调性,这里可以具体展开看看。
首先简述一下原始动态规划的思路:
1、暴力穷举尝试在所有楼层 1 <= i <= N 扔鸡蛋,每次选择尝试次数最少的那一层;
2、每次扔鸡蛋有两种可能,要么碎,要么没碎;
3、如果鸡蛋碎了,F 应该在第 i 层下面,否则,F 应该在第 i 层上面;
4、鸡蛋是碎了还是没碎,取决于哪种情况下尝试次数更多,因为我们想求的是最坏情况下的结果。
核心的状态转移代码是这段:
# 当前状态为 K 个鸡蛋,面对 N 层楼# 返回这个状态下的最优结果def dp(K, N):for 1 <= i <= N:# 最坏情况下的最少扔鸡蛋次数res = min(res,max(dp(K - 1, i - 1), # 碎dp(K, N - i) # 没碎) + 1 # 在第 i 楼扔了一次)return res
这个 for 循环就是下面这个状态转移方程的具体代码实现:
如果能够理解这个状态转移方程,那么就很容易理解二分查找的优化思路。
首先我们根据 dp(K, N) 数组的定义(有 K 个鸡蛋面对 N 层楼,最少需要扔几次),很容易知道 K 固定时,这个函数随着 N 的增加一定是单调递增的,无论你策略多聪明,楼层增加测试次数一定要增加。
那么注意 dp(K - 1, i - 1) 和 dp(K, N - i) 这两个函数,其中 i 是从 1 到 N 单增的,如果我们固定 K 和 N,把这两个函数看做关于 i 的函数,前者随着 i 的增加应该也是单调递增的,而后者随着 i 的增加应该是单调递减的:
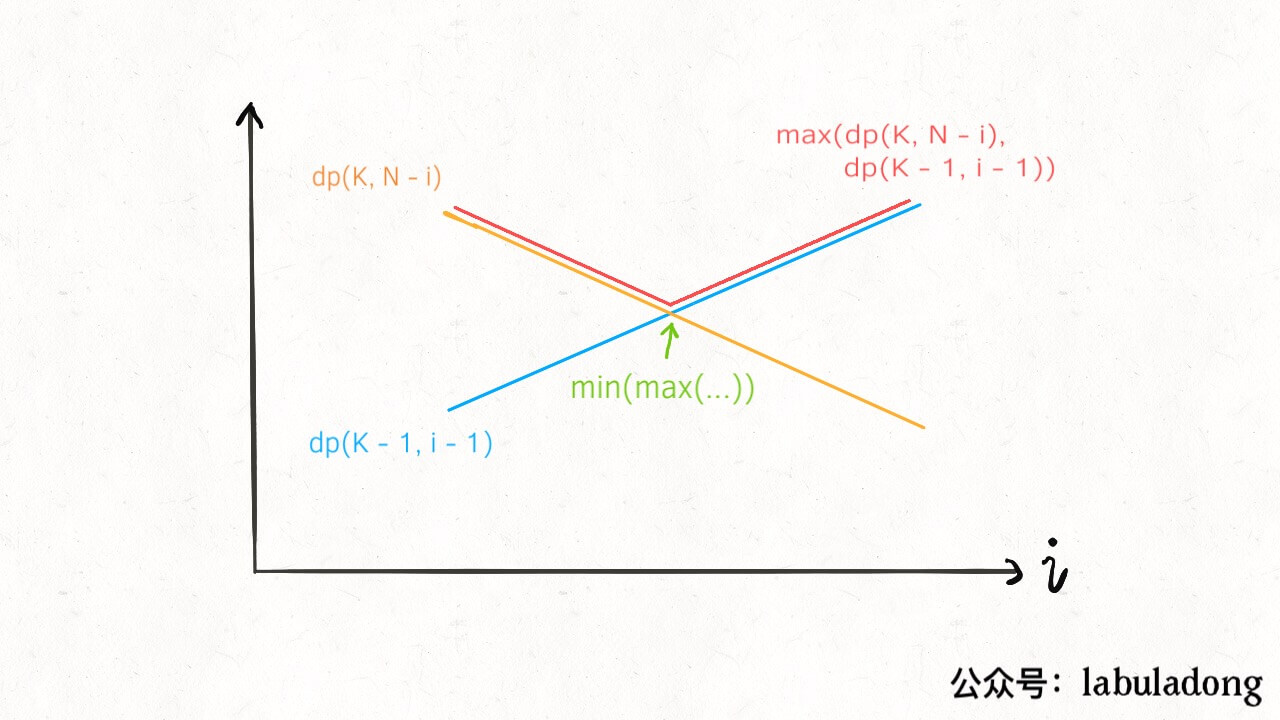
这时候求二者的较大值,再求这些最大值之中的最小值,其实就是求这两条直线交点,也就是红色折线的最低点嘛。
我们前文「二分查找只能用来查找元素吗」讲过,二分查找的运用很广泛,形如下面这种形式的 for 循环代码:
for (int i = 0; i < n; i++) {if (isOK(i))return i;}
都很有可能可以运用二分查找来优化线性搜索的复杂度,回顾这两个 dp 函数的曲线,我们要找的最低点其实就是这种情况:
for (int i = 1; i <= N; i++) {if (dp(K - 1, i - 1) == dp(K, N - i))return dp(K, N - i);}
熟悉二分搜索的同学肯定敏感地想到了,这不就是相当于求 Valley(山谷)值嘛,可以用二分查找来快速寻找这个点的,直接看代码吧,整体的思路还是一样,只是加快了搜索速度:
def superEggDrop(self, K: int, N: int) -> int:memo = dict()def dp(K, N):if K == 1: return Nif N == 0: return 0if (K, N) in memo:return memo[(K, N)]# for 1 <= i <= N:# res = min(res,# max(# dp(K - 1, i - 1),# dp(K, N - i)# ) + 1# )res = float('INF')# 用二分搜索代替线性搜索lo, hi = 1, Nwhile lo <= hi:mid = (lo + hi) // 2broken = dp(K - 1, mid - 1) # 碎not_broken = dp(K, N - mid) # 没碎# res = min(max(碎,没碎) + 1)if broken > not_broken:hi = mid - 1res = min(res, broken + 1)else:lo = mid + 1res = min(res, not_broken + 1)memo[(K, N)] = resreturn resreturn dp(K, N)
这个算法的时间复杂度是多少呢?动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度。
函数本身的复杂度就是忽略递归部分的复杂度,这里 dp 函数中用了一个二分搜索,所以函数本身的复杂度是 O(logN)。
子问题个数也就是不同状态组合的总数,显然是两个状态的乘积,也就是 O(KN)。
所以算法的总时间复杂度是 O(K*N*logN), 空间复杂度 O(KN)。效率上比之前的算法 O(KN^2) 要高效一些。
重新定义状态转移
前文「不同定义有不同解法」就提过,找动态规划的状态转移本就是见仁见智,比较玄学的事情,不同的状态定义可以衍生出不同的解法,其解法和复杂程度都可能有巨大差异。这里就是一个很好的例子。
再回顾一下我们之前定义的 dp 数组含义:
def dp(k, n) -> int# 当前状态为 k 个鸡蛋,面对 n 层楼# 返回这个状态下最少的扔鸡蛋次数
用 dp 数组表示的话也是一样的:
dp[k][n] = m# 当前状态为 k 个鸡蛋,面对 n 层楼# 这个状态下最少的扔鸡蛋次数为 m
按照这个定义,就是确定当前的鸡蛋个数和面对的楼层数,就知道最小扔鸡蛋次数。最终我们想要的答案就是 dp(K, N) 的结果。
这种思路下,肯定要穷举所有可能的扔法的,用二分搜索优化也只是做了「剪枝」,减小了搜索空间,但本质思路没有变,还是穷举。
现在,我们稍微修改 dp 数组的定义,确定当前的鸡蛋个数和最多允许的扔鸡蛋次数,就知道能够确定 F 的最高楼层数。具体来说是这个意思:
dp[k][m] = n# 当前有 k 个鸡蛋,可以尝试扔 m 次鸡蛋# 这个状态下,最坏情况下最多能确切测试一栋 n 层的楼# 比如说 dp[1][7] = 7 表示:# 现在有 1 个鸡蛋,允许你扔 7 次;# 这个状态下最多给你 7 层楼,# 使得你可以确定楼层 F 使得鸡蛋恰好摔不碎# (一层一层线性探查嘛)
这其实就是我们原始思路的一个「反向」版本,我们先不管这种思路的状态转移怎么写,先来思考一下这种定义之下,最终想求的答案是什么?
我们最终要求的其实是扔鸡蛋次数 m,但是这时候 m 在状态之中而不是 dp 数组的结果,可以这样处理:
int superEggDrop(int K, int N) {int m = 0;while (dp[K][m] < N) {m++;// 状态转移...}return m;}
题目不是给你 K 鸡蛋,N 层楼,让你求最坏情况下最少的测试次数 m 吗?while 循环结束的条件是 dp[K][m] == N,也就是给你 K 个鸡蛋,测试 m 次,最坏情况下最多能测试 N 层楼。
注意看这两段描述,是完全一样的!所以说这样组织代码是正确的,关键就是状态转移方程怎么找呢?还得从我们原始的思路开始讲。之前的解法配了这样图帮助大家理解状态转移思路:
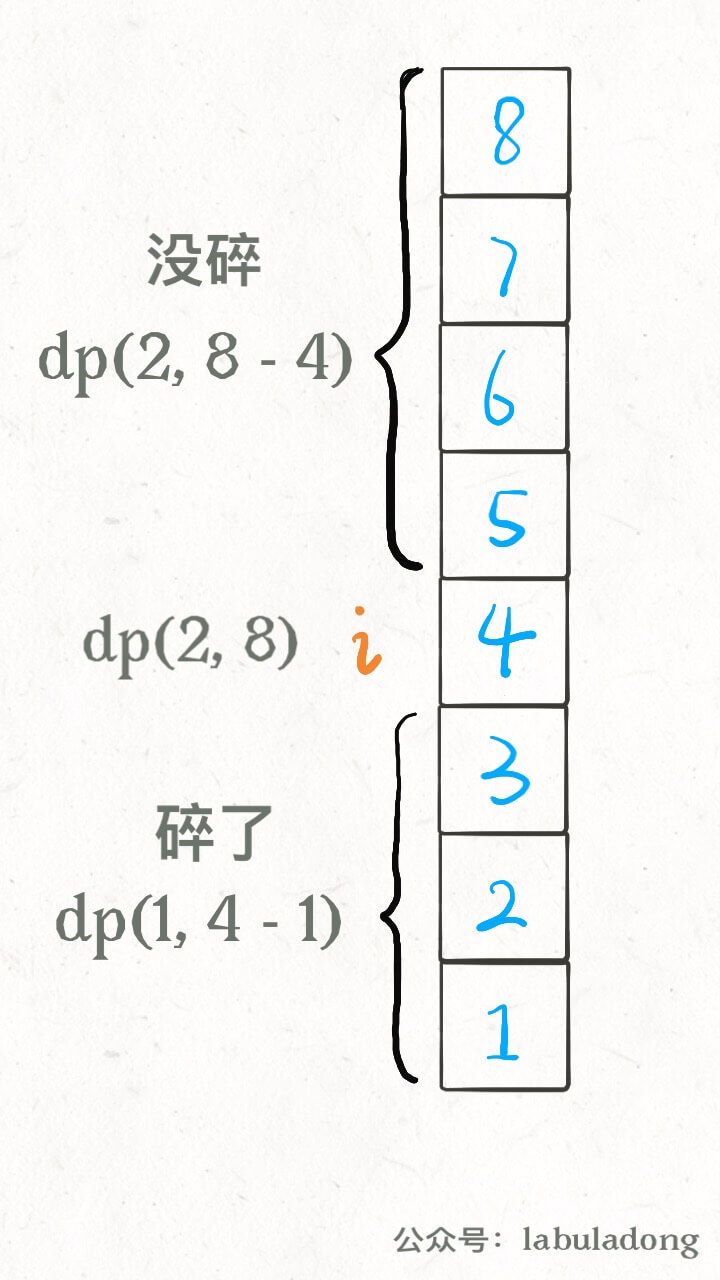
这个图描述的仅仅是某一个楼层 i,原始解法还得线性或者二分扫描所有楼层,要求最大值、最小值。但是现在这种 dp 定义根本不需要这些了,基于下面两个事实:
1、无论你在哪层楼扔鸡蛋,鸡蛋只可能摔碎或者没摔碎,碎了的话就测楼下,没碎的话就测楼上。
2、无论你上楼还是下楼,总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1(当前这层楼)。
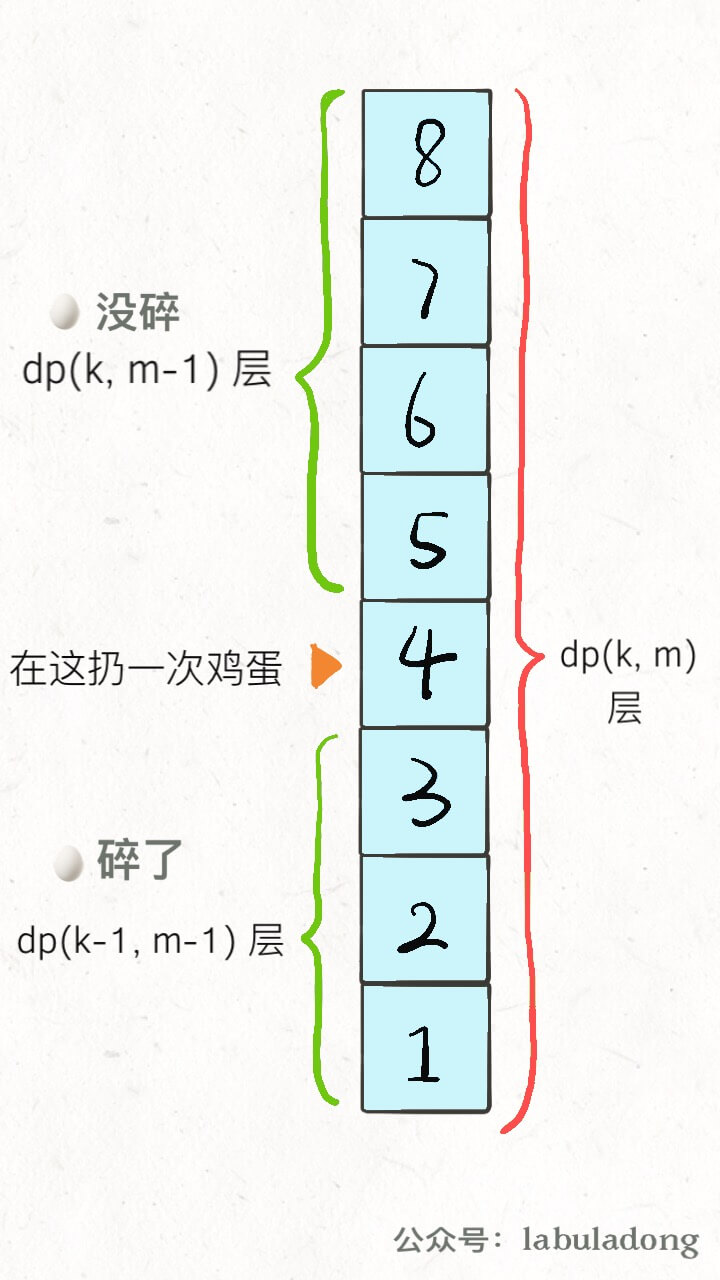
根据这个特点,可以写出下面的状态转移方程:
dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1
dp[k][m - 1] 就是楼上的楼层数,因为鸡蛋个数 k 不变,也就是鸡蛋没碎,扔鸡蛋次数 m 减一;
dp[k - 1][m - 1] 就是楼下的楼层数,因为鸡蛋个数 k 减一,也就是鸡蛋碎了,同时扔鸡蛋次数 m 减一。
PS:这个 m 为什么要减一而不是加一?之前定义得很清楚,这个 m 是一个允许的次数上界,而不是扔了几次。
至此,整个思路就完成了,只要把状态转移方程填进框架即可:
int superEggDrop(int K, int N) {// m 最多不会超过 N 次(线性扫描)int[][] dp = new int[K + 1][N + 1];// base case:// dp[0][..] = 0// dp[..][0] = 0// Java 默认初始化数组都为 0int m = 0;while (dp[K][m] < N) {m++;for (int k = 1; k <= K; k++)dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;}return m;}
如果你还觉得这段代码有点难以理解,其实它就等同于这样写:
for (int m = 1; dp[K][m] < N; m++)for (int k = 1; k <= K; k++)dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1;
看到这种代码形式就熟悉多了吧,因为我们要求的不是 dp 数组里的值,而是某个符合条件的索引 m,所以用 while 循环来找到这个 m 而已。
这个算法的时间复杂度是多少?很明显就是两个嵌套循环的复杂度 O(KN)。
另外注意到 dp[m][k] 转移只和左边和左上的两个状态有关,所以很容易优化成一维 dp 数组,这里就不写了。
还可以再优化
再往下就要用一些数学方法了,不具体展开,就简单提一下思路吧。
在刚才的思路之上,注意函数 dp(m, k) 是随着 m 单增的,因为鸡蛋个数 k 不变时,允许的测试次数越多,可测试的楼层就越高。
这里又可以借助二分搜索算法快速逼近 dp[K][m] == N 这个终止条件,时间复杂度进一步下降为 O(KlogN),我们可以设 g(k, m) =……
算了算了,打住吧。我觉得我们能够写出 O(K*N*logN) 的二分优化算法就行了,后面的这些解法呢,听个响鼓个掌就行了,把欲望限制在能力的范围之内才能拥有快乐!
不过可以肯定的是,根据二分搜索代替线性扫描 m 的取值,代码的大致框架肯定是修改穷举 m 的 for 循环:
// 把线性搜索改成二分搜索// for (int m = 1; dp[K][m] < N; m++)int lo = 1, hi = N;while (lo < hi) {int mid = (lo + hi) / 2;if (... < N) {lo = ...} else {hi = ...}for (int k = 1; k <= K; k++)// 状态转移方程}
简单总结一下吧,第一个二分优化是利用了 dp 函数的单调性,用二分查找技巧快速搜索答案;第二种优化是巧妙地修改了状态转移方程,简化了求解了流程,但相应的,解题逻辑比较难以想到;后续还可以用一些数学方法和二分搜索进一步优化第二种解法,不过看了看镜子中的发量,算了。
本文终,希望对你有一点启发。
